采集矿石题解

一句话题意:给定一个字符串和其每个位置相应的权值，求满足以下条件的子串个数:
1. 子串所对应的权值和等于其在所有字串中的排名(从大到小)
  
  (也就是第K大的子串权值和为K)
2. 注意:相同的子串排名时算一个，但统计答案是分开算。
30pts做法

~~(暴力模拟)~~

正解

首先看到是字符串的题，又没有匹配问题，那么肯定就和后缀有关了。~~(因为我只会这么多)~~

考虑后缀数组。

我们考虑如何用后缀数组求一个串的本质不同的子串个数。

一个串的本质不同的子串个数应为

$ \sum_{i=1}^{n} n-sa[i]-height[i]+1 $

观察题目中的条件，可以发现若固定一个起始点，那么从它的开始的后缀的排名时单调下降的，而因为权值为非负的，所以子串的权值和是单调不降的，大概如下图所示。

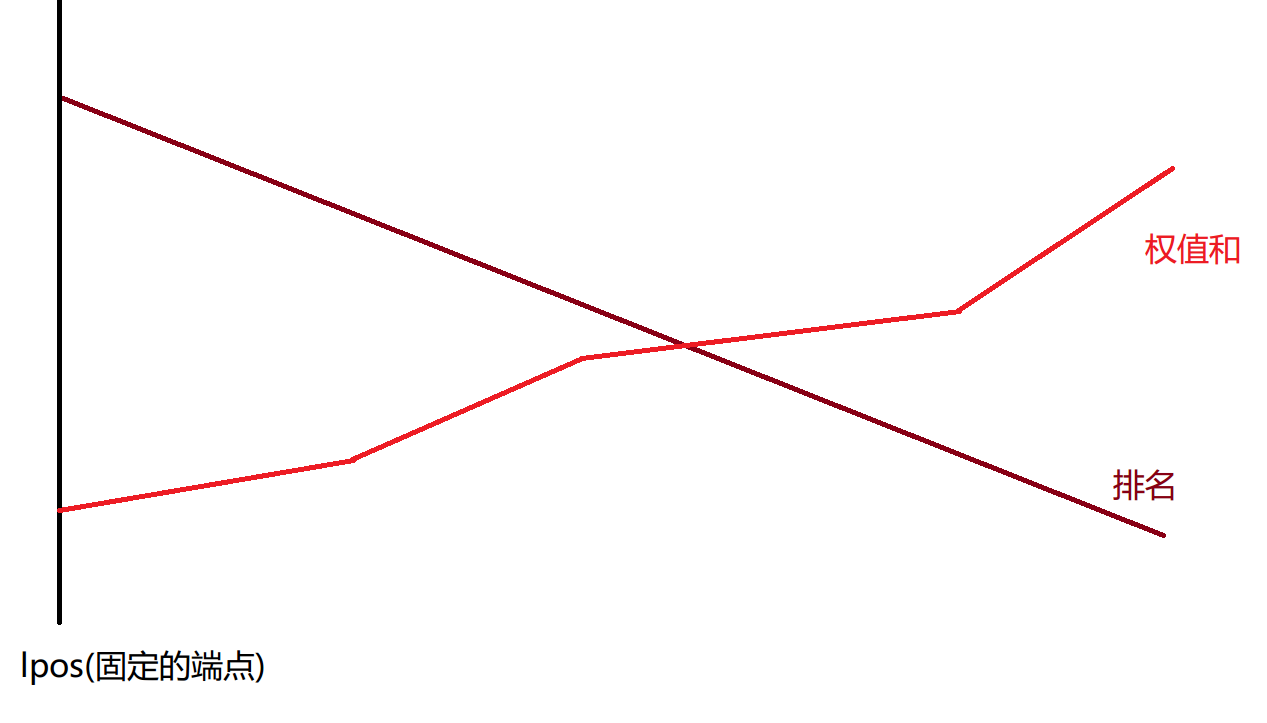
接下来，我们就可以二分这个交点，如果有交点，那么 $ ans++ $ ，并记录当前方案，否则枚举下一个端点。

并且如果按照Rank的顺序来枚举，可以发现一个后缀之前的子串个数是可以用前缀和进行优化的。

经过 ~~严谨的~~ 推导，可以得出一个子串 $ (lpos,r) $ 的排名为 $ sum[n]-(sum[Rank[lpos]-1]+pos-lpos-height[Rank[lpos]]) $ 。

注意：这个式子仅适用于该子串不是与当前串的前一个排名的串的LCP的子串时成立。

即该式当且仅当 $ pos-lpos+1>height[Rank[lpos]] $ 时成立。

接下来考虑如何处理 $ LCP $ 部分。

第一个思路：

开一个临时数组，记一下前面 $ LCP $ 部分的 $ Rank $ 然后在枚举时每次看一下当前临时数组的大小的 $ Height[i+1] $ 的大小，来判断是否需要更新临时数组。如果 $ size<height[i+1] $ 那么暴力更新临时数组，直至 $ size=height[i+1] $。

可以发现，这种暴力处理的复杂度有可能被卡成 $ O(n^2) $。

这个思路的得分为76分

第二个思路：

依照第一的思路，可以发现你要更新的这一段其实是一段连续下降的序列，且公差是 $ 1 $。

可以使用线段树，该线段树支持区间赋值和区间加等差数列。

也可以在线段树上维护这个位置所在增加的 $ LCP $ 的第一个位置，然后只在临时数组中记一下每次增加的第一位置的 $ Rank $ ，之后可以通过位置计算出当前位置的 $ Rank $ 。

现在已经处理完了 $ LCP $ 部分的 $ Rank $ 了。我们发现，其实 $ LCP $ 部分的 $ Rank $ 也是单调下降的，这样我们可以在处理非 $ LCP $ 部分时一起二分。

总复杂度 : $ O(nlogn) $

至此，该问题已被完全解决。

STD:

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<bitset>
#include<ctime>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define get_val(l,r) sumv[r]-sumv[l-1]
const int MAXN=100010;
struct O{
    int l,r;
    bool operator < (O a)
    {
        return l<a.l;
    }
}ot[MAXN];
int t[MAXN<<2];
inline void pushup(int x)
{
    t[x]=t[x<<1]*(t[x<<1]==t[x<<1|1]);
}
inline void pushdown(int x,int l,int r)
{
    if(!t[x])
        return;
    t[x<<1]=t[x<<1|1]=t[x];
}
inline void change(int x,int l,int r,int ql,int qr,int val)
{
    if(ql>r||qr<l)
        return;
    if(ql<=l&&r<=qr){
        t[x]=val+1;
        return;
    }
    pushdown(x,l,r);
    int mid=(l+r)>>1;
    if(ql<=mid)
        change(x<<1,l,mid,ql,qr,val);
    if(qr>=mid+1)
        change(x<<1|1,mid+1,r,ql,qr,val);
    pushup(x);
}
inline int query(int x,int l,int r,int pos)
{
    if(t[x])
        return t[x]-1;
    pushdown(x,l,r);
    int mid=(l+r)>>1;
    if(pos<=mid)
        return query(x<<1,l,mid,pos);
    else
        return query(x<<1|1,mid+1,r,pos);
}
char str[MAXN];
ll Rank[MAXN],sa[MAXN];
ll sum[MAXN],tp[MAXN];
ll height[MAXN],h[MAXN];
ll val[MAXN],sumv[MAXN];
ll tmprank[MAXN],tot;
int n;
ll ans=0;
void get_sa(int n)
{
    int m=127;
    for(int i=1;i<=n;i++) Rank[i]=str[i],tp[i]=i;
    for(int i=0;i<=m;i++) sum[i]=0;
    for(int i=1;i<=n;i++) sum[Rank[tp[i]]]++;
    for(int i=1;i<=m;i++) sum[i]+=sum[i-1];
    for(int i=n;i>=1;i--) sa[sum[Rank[tp[i]]]--]=tp[i];
    int p=1;
    for(int len=1;p<n;len<<=1,m=p)
    {
        p=0;
        for(int i=n-len+1;i<=n;i++) tp[++p]=i;
        for(int i=1;i<=n;i++) if(sa[i]>len) tp[++p]=sa[i]-len;
        for(int i=0;i<=m;i++) sum[i]=0;
        for(int i=1;i<=n;i++) sum[Rank[tp[i]]]++;
        for(int i=1;i<=m;i++) sum[i]+=sum[i-1];
        for(int i=n;i>=1;i--) sa[sum[Rank[tp[i]]]--]=tp[i];
        swap(Rank,tp);Rank[sa[1]]=1;p=1;
        for(int i=2;i<=n;i++)
            Rank[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+len]==tp[sa[i-1]+len])?p:++p;
    }
    int lst=0,j;
    for(int i=1;i<=n;h[i]=lst,height[Rank[i++]]=lst)
        for(lst=lst?lst-1:lst,j=sa[Rank[i]-1];str[j+lst]==str[i+lst];++lst);
}
int get_rank(int lpos,int pos)
{
    if(pos-lpos+1>height[Rank[lpos]]) return sum[n]-(sum[Rank[lpos]-1]+pos-lpos-height[Rank[lpos]]);
    else
    {
        int pre=query(1,1,n,pos-lpos+1);
        return tmprank[pre]+pre-(pos-lpos+1);
    }
}
int tttt;
int main()
{
    scanf("%s",str+1);
    n=strlen(str+1);
    for(int i=1;i<=n;i++)
        scanf("%lld",&val[i]),sumv[i]=sumv[i-1]+val[i];
    get_sa(n);
    for(int i=1;i<=n;i++)
        sum[i]=n-sa[i]-height[i]+1+sum[i-1];
    for(int i=1;i<=n;i++) //枚举Rank
    {
        int L=sa[i],R=n,lpos=sa[i];
        while(L<R)
        {
            int mid=(L+R)>>1;
            if(get_val(lpos,mid)<get_rank(lpos,mid))
                L=mid+1;
            else R=mid;
        }

        if(get_val(lpos,L)==get_rank(lpos,L))
            ot[++ans]={lpos,L};
        if(i!=n&&height[i]<height[i+1])
            tmprank[height[i]+1]=get_rank(sa[i],sa[i]+height[i]),
            change(1,1,n,height[i]+1,height[i+1],height[i]+1);
    }
    sort(ot+1,ot+1+ans);
    printf("%lld\n",ans);
    for(int i=1;i<=ans;i++)
        printf("%d %d\n",ot[i].l,ot[i].r);
}